How to Use Compressive Stress Formula in Structural Design
Ever wonder how skyscrapers stand tall against the crushing weight of gravity, or how a bridge supports tons of traffic without buckling? A key factor is understanding and applying the compressive stress formula. It's a fundamental principle in structural design, ensuring the safety and stability of countless structures around us. For engineers, students diving into mechanical engineering, and professionals working with material strength, mastering this formula is non-negotiable.
Understanding Compressive Stress
Compressive stress is what happens when a force tries to squash or compress a material. Think of squeezing a sponge – the force you apply creates compressive stress within the sponge. Understanding this stress is vital for predicting whether a material will deform or fail under load, a critical aspect of failure analysis in structural design.
In contrast to tensile stress (which stretches a material), compressive stress shortens it. Both tensile and compressive stress are crucial considerations when designing structures, as materials often experience both simultaneously.
Defining Compressive Stress
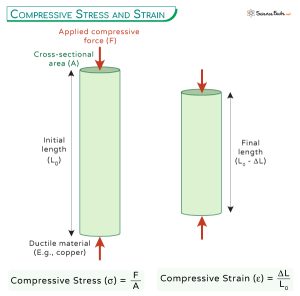
Compressive stress (σc) is defined as the force (F) applied perpendicular to a surface divided by the area (A) over which that force is distributed. Mathematically, it's expressed as: σc = F/A. The SI unit for stress is Pascal (Pa), which is equivalent to N/m2. However, in many engineering applications, megapascals (MPa) or kilopounds per square inch (ksi) are used.
Deriving the Compressive Stress Formula
The derivation is straightforward. It starts with the basic understanding that stress is force per unit area. Imagine a column supporting a weight. The weight (force) is distributed across the cross-sectional area of the column. Therefore, the compressive stress within the column is simply the weight divided by that area. A deeper dive involves considering the material's properties and potential buckling, which we'll touch on later.
Applying the Compressive Stress Formula: A Step-by-Step Guide
Now, let’s walk through how to actually use the compressive stress formula in a practical scenario. We’ll break it down into clear, manageable steps.
This example focuses on a simple column, but the principles apply to more complex structures as well. Just remember to carefully consider the forces and areas involved.
Step 1: Identify the Compressive Force (F)
The first step is to determine the magnitude and direction of the force acting on the object. This force must be compressive, meaning it’s pushing or squeezing the material. If multiple forces are present, calculate the net compressive force acting perpendicular to the area of interest. Make sure you’re using consistent units (e.g., Newtons or pounds).
Step 2: Determine the Cross-Sectional Area (A)
Next, calculate the cross-sectional area of the object that’s resisting the compressive force. The area must be perpendicular to the direction of the force. For a rectangular column, this would be length times width. For a circular column, it's πr2, where r is the radius. Again, maintain consistent units (e.g., m2 or in2).
Step 3: Apply the Formula: σc = F/A
Now, simply divide the compressive force (F) by the cross-sectional area (A) to calculate the compressive stress (σc). Make sure your units are compatible to get the stress in the correct units (Pascals, MPa, or ksi).
Step 4: Interpret the Result
The compressive stress value tells you how much force is being distributed over each unit of area. This value is then compared to the material's compressive strength – the maximum compressive stress the material can withstand before failing. If the calculated compressive stress is lower than the compressive strength, the structure should be safe under that load. However, it's crucial to consider safety factors, potential imperfections, and other failure modes like buckling.
Example Calculation
Let's say we have a concrete column with a cross-sectional area of 0.25 m2 supporting a load of 500,000 N. What is the compressive stress on the column?
Using the formula σc = F/A, we have: σc = 500,000 N / 0.25 m2 = 2,000,000 Pa or 2 MPa. Now, let's say the compressive strength of the concrete is 25 MPa. Since the calculated stress (2 MPa) is significantly less than the compressive strength (25 MPa), the column is likely safe under this load. However, this doesn’t account for potential buckling or other failure modes; a thorough structural analysis is always necessary.
Compressive Stress vs. Compressive Strength
Understanding the difference between compressive stress and compressive strength is crucial. Compressive stress is the stressexperiencedby the material under a load. Compressive strength, on the other hand, is a material property representing the maximum compressive stress the material canwithstandbefore failure (yielding or fracture).
Structural designs must ensure that the calculated compressive stress is always significantly lower than the material's compressive strength, incorporating a safety factor to account for uncertainties and potential overloads. Ignoring this distinction can lead to catastrophic failures.
Limitations and Considerations
While the compressive stress formula is fundamental, it has limitations. It assumes a uniform distribution of stress, which might not always be the case in real-world scenarios. Stress concentrations can occur at corners, holes, or other geometric discontinuities, leading to higher stresses in localized areas. Furthermore, the formula doesn't account for buckling, a failure mode common in slender columns subjected to compression. Buckling occurs when the column bends or collapses sideways, even if the compressive stress is below the material's compressive strength.
Practical Applications and Case Studies
The compressive stress formula is used extensively in various engineering fields. In civil engineering, it's used to design bridges, buildings, and other infrastructure. In mechanical engineering, it's used to design machine components, pressure vessels, and aerospace structures. Here are a few examples:
Bridge Design: Calculating the compressive stress in bridge piers and supports to ensure they can withstand the weight of vehicles and the bridge itself.
Building Construction: Determining the size and material of columns and walls to support the weight of the building and its occupants.
Aircraft Design: Analyzing the compressive stress in fuselage components to ensure they can withstand aerodynamic loads during flight.
Pros and Cons of Using the Compressive Stress Formula
Like any tool, the compressive stress formula has its strengths and weaknesses.
Pros: Simplicity: The formula is easy to understand and apply. Fundamental: Provides a foundational understanding of stress analysis. Widely Applicable: Used in numerous engineering applications.
Cons: Assumptions: Assumes uniform stress distribution, which isn't always accurate. Ignores Buckling: Doesn't account for buckling failure. Simplification: May not be sufficient for complex geometries or loading conditions.
Frequently Asked Questions
What is the difference between compressive stress and strain?
Compressive stress is the force per unit area that a material experiences when subjected to a compressive load. Compressive strain, on the other hand, is the deformation of the material (change in length divided by the original length) caused by that stress. Stress causes strain.
How does temperature affect compressive strength?
Generally, higher temperatures tend to reduce the compressive strength of most materials. This is because increased temperature can weaken the interatomic bonds within the material.
What is a safety factor, and why is it important?
A safety factor is a multiplier applied to the calculated stress to ensure that the actual stress remains below the material's strength. It accounts for uncertainties in material properties, loading conditions, and manufacturing imperfections. It's crucial for ensuring the safety and reliability of structures.
Can the compressive stress formula be used for materials other than solids?
While primarily used for solid materials, the concept of compressive stress can be extended to fluids under specific conditions, such as in hydraulic systems or confined gases. However, the behavior of fluids under compression is more complex and requires specialized analysis.
What are some common units for measuring compressive stress?
Common units include Pascal (Pa), megapascals (MPa), kilopounds per square inch (ksi), and pounds per square inch (psi).
How does the shape of a structure affect its compressive strength?
The shape significantly affects compressive strength. For example, slender columns are more prone to buckling than short, squat columns. Geometric features like curves and corners can also create stress concentrations, weakening the structure. Optimized shapes, like those found in I-beams, can distribute stress more evenly, increasing strength.
Conclusion
The compressive stress formula is an indispensable tool for anyone involved in structural design and mechanical engineering. Understanding its principles, applications, and limitations allows engineers to create safe, reliable, and efficient structures. While it's a fundamental concept, remember that real-world applications often require more sophisticated analysis to account for complex geometries, loading conditions, and potential failure modes. Keep learning, keep exploring, and keep building!
Posting Komentar untuk "How to Use Compressive Stress Formula in Structural Design"