Applications of Compressive Stress Formula in Columns
Ever wonder how skyscrapers manage to stand tall against gravity, or how the legs of a heavy table don't buckle under pressure? The answer, in part, lies in understanding and applying the compressive stress formula, especially when dealing with columns. Mastering this concept is crucial for engineers, architects, and anyone involved in structural design because it directly impacts the safety and stability of structures.
Understanding Compressive Stress
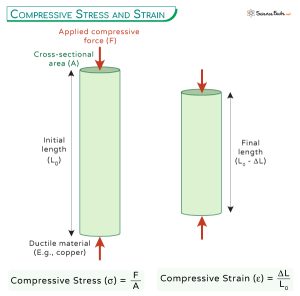
Compressive stress is what happens when a force is applied to an object, causing it to be squeezed or compressed. Imagine pushing down on a block of foam – you're creating compressive stress within the material. Columns, by their very nature, are designed to withstand this type of stress, supporting loads from above.
In mechanical engineering, the accurate calculation of compressive stress is paramount. It helps us determine whether a column can handle the intended load without failing. Ignoring this calculation can lead to catastrophic structural failures, emphasizing the importance of a solid understanding of the underlying principles.
What is the Compressive Stress Formula?
The formula for compressive stress is relatively straightforward: σ = F/A, where:
- σ (sigma) represents the compressive stress (usually measured in Pascals (Pa) or pounds per square inch (psi)).
- F represents the applied force (measured in Newtons (N) or pounds (lb)).
- A represents the cross-sectional area of the column (measured in square meters (m²) or square inches (in²)).
This formula tells us that the stress experienced by a column is directly proportional to the applied force and inversely proportional to the cross-sectional area. A larger force results in greater stress, while a larger area distributes the force more effectively, reducing stress.
Derivation of the Formula
The compressive stress formula is derived from the basic definition of stress as force per unit area. Imagine a uniform force acting perpendicularly over a surface. The intensity of this force over that area is what we define as stress. In the context of compression, this force is pushing inwards on the material.
Practical Applications in Structural Design
The compressive stress formula finds wide-ranging application in structural design. Here are some key areas where it's indispensable:
- Building Construction: Ensuring the pillars and supporting beams can withstand the weight of the building and its occupants.
- Bridge Design: Calculating the load-bearing capacity of bridge supports and piers.
- Machine Design: Designing components like piston rods and connecting rods that experience compressive forces.
- Aerospace Engineering: Analyzing the stress on aircraft landing gear and fuselage components.
Case Study: Designing a Support Column
Let's say we need to design a cylindrical steel column to support a load of 500,000 N. The steel has a compressive strength of 250 MPa (megapascals). We need to determine the minimum required diameter of the column.
First, we use the compressive stress formula: σ = F/A. We know σ (250 MPa = 250 x 10^6 Pa) and F (500,000 N). We need to find A.
Rearranging the formula, we get A = F/σ = 500,000 N / (250 x 10^6 Pa) = 0.002 m².
Since the column is cylindrical, its area is A = πr², where r is the radius. Solving for r, we get r = √(A/π) = √(0.002 m² / π) ≈
0.0252 m.
Finally, the diameter is twice the radius: d = 2r ≈ 0.0504 m, or
50.4 mm. Therefore, the minimum required diameter for the steel column is approximately
50.4 mm to safely support the 500,000 N load.
Comparing Materials: Steel vs. Concrete
Steel and concrete are commonly used materials for columns, but they behave differently under compressive stress. Steel is strong in both tension and compression, while concrete is significantly weaker in tension. Therefore, concrete columns are often reinforced with steel rebar to improve their tensile strength and overall load-bearing capacity.
Steel columns are generally more slender than concrete columns for the same load, due to steel's higher strength-to-weight ratio. However, concrete is more cost-effective for larger structures where volume is not a primary constraint.
Pros and Cons of Using the Compressive Stress Formula
Like any engineering tool, the compressive stress formula has its strengths and limitations.
Pros:
- Simple and Effective: The formula is easy to understand and apply for basic calculations.
- Predictive Power: It provides a reliable estimate of the stress experienced by a column under load.
- Material Selection: It helps engineers choose appropriate materials based on their compressive strength.
Cons:
- Simplified Model: It assumes uniform stress distribution, which may not be accurate in complex geometries or loading conditions.
- Ignores Buckling: It doesn't account for buckling, a form of instability that can occur in slender columns.
- Idealized Conditions: It assumes ideal material properties and doesn't factor in imperfections or defects.
For more complex scenarios, finite element analysis (FEA) software is often used to simulate stress distribution and buckling behavior more accurately.
FAQs about Compressive Stress in Columns
What is buckling and how does it differ from compressive stress?
Buckling is a form of instability that occurs in slender columns under compression. Instead of simply crushing, the column bends or deflects laterally. Compressive stress is the internal stress within the material, while buckling is a mode of failure influenced by the column's geometry and material properties.
How does the length of a column affect its compressive strength?
The length of a column significantly affects its compressive strength. Longer columns are more susceptible to buckling and have a lower critical load-bearing capacity. This relationship is captured by Euler's buckling formula, which considers the column's length, material properties, and end conditions.
What are the different types of column end conditions and how do they affect calculations?
Column end conditions refer to how the ends of the column are supported (e.g., fixed, pinned, free). These conditions affect the column's effective length, which is used in buckling calculations. Different end conditions result in different effective lengths and, consequently, different buckling loads.
Is the compressive stress formula applicable to materials other than steel and concrete?
Yes, the compressive stress formula is applicable to any material that experiences compressive forces, including wood, aluminum, polymers, and composites. However, it's crucial to use the appropriate material properties (e.g., compressive strength, modulus of elasticity) in the calculations.
How can I improve the compressive strength of a column?
Several strategies can be used to improve the compressive strength of a column, including increasing its cross-sectional area, using a material with higher compressive strength, shortening its length, or providing additional support to prevent buckling.
What is the safety factor and why is it important in compressive stress calculations?
The safety factor is a multiplier applied to the calculated stress or load to account for uncertainties in material properties, loading conditions, and design assumptions. It ensures that the actual stress on the column remains below its compressive strength, providing a margin of safety against failure. A higher safety factor results in a more conservative design.
Conclusion
Understanding the compressive stress formula is a fundamental skill for anyone involved in structural design. While the formula itself is simple, its applications are far-reaching, impacting the safety and stability of everything from buildings and bridges to machines and aircraft. Remember to consider the limitations of the formula and use it in conjunction with other engineering principles and tools for more complex scenarios. By mastering this concept, you'll be well-equipped to design safer and more efficient structures.
Posting Komentar untuk "Applications of Compressive Stress Formula in Columns"