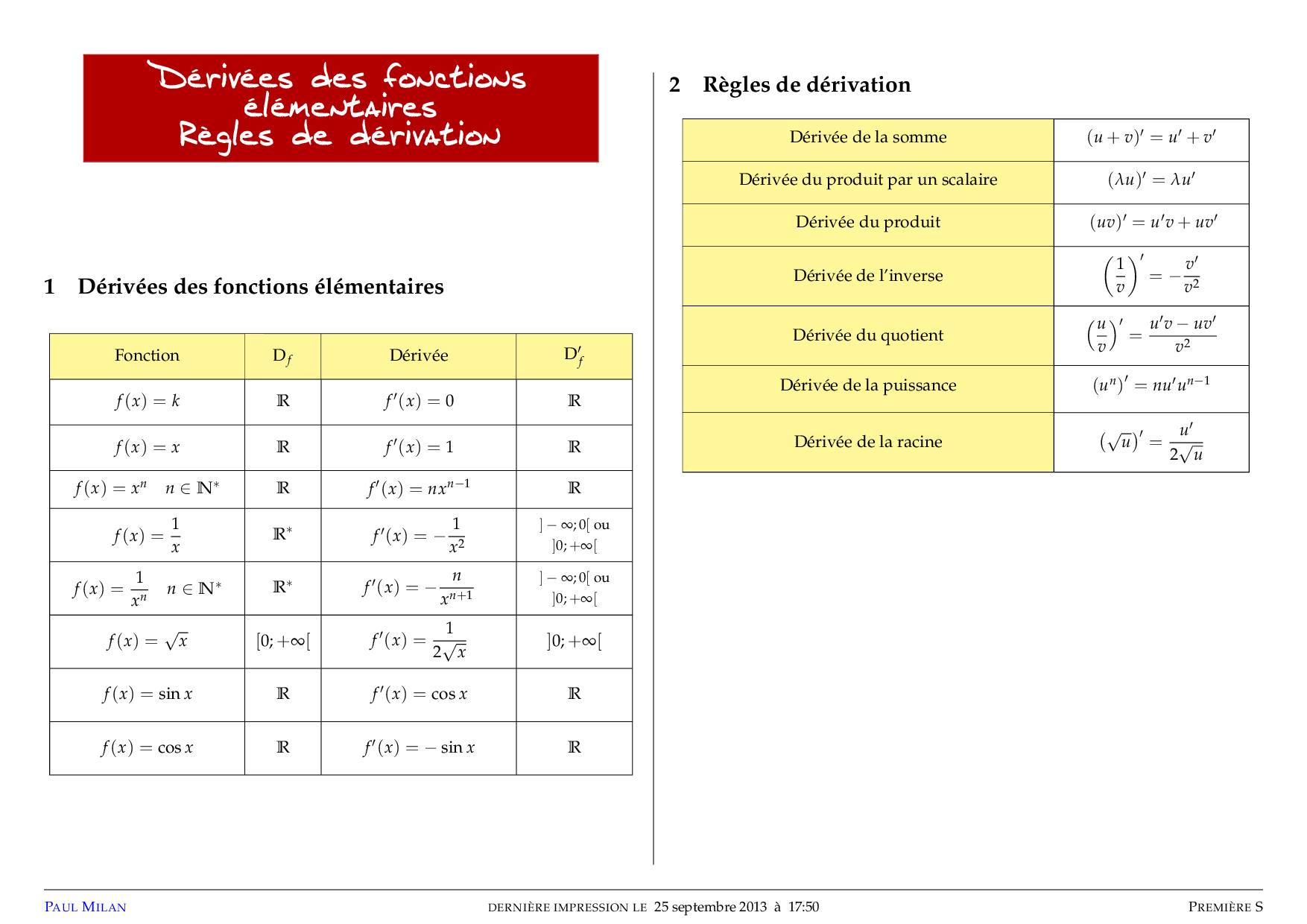
Derivation of Maximum Stress Formula in Mechanics
Ever wondered how engineers ensure that a bridge can withstand heavy traffic or an airplane wing can endure turbulent flights? It all boils down to understanding stress within materials. Knowing the maximum stress a component can handle is crucial for preventing catastrophic failures in mechanical engineering. This formula is a cornerstone for material selection and structural design, saving lives and resources by ensuring the integrity of our built environment.
Understanding Stress: The Foundation
Stress, in the context of mechanics, is the force acting per unit area within a material. It's a measure of the internal forces that molecules within a continuous material exert on each other. Understanding stress is paramount in structural design to ensure components can withstand applied loads without failing. We’ll break down the concepts of tensile and compressive stress, which will be important to understand the maximum stress formula later.
Tensile and Compressive Stress
Tensile stress occurs when a material is pulled apart, like when you stretch a rubber band. It's a pulling force acting over an area. Compressive stress, on the other hand, happens when a material is squeezed or compressed, similar to stacking books on top of each other. It's a pushing force acting over an area. Both are critical considerations in determining the overall stress state within a component and in failure analysis.
Shear Stress
Shear stress arises when forces act parallel to a surface, causing one part of the material to slide relative to another. Think of cutting paper with scissors; the force applied is creating shear stress within the paper. Although we're focusing on tensile/compressive stress for the max stress formula here, shear stress also plays a significant role in overall structural integrity.
The Maximum Stress Formula: A Deep Dive
The maximum stress formula helps us determine the highest stress value within a material subjected to various loads. While the specific formula varies depending on the loading conditions and geometry, the general concept involves identifying the critical point within the material where stress is concentrated. Let's explore a common scenario: axial loading of a bar.
Axial Loading: A Simple Case
Consider a bar with a uniform cross-sectional area (A) subjected to an axial force (F). The stress (σ) is uniformly distributed across the cross-section and can be calculated as: σ = F/A. In this simplified scenario, the maximum stress is simply equal to this calculated stress, assuming the load is perfectly aligned and there are no stress concentrators. However, real-world situations are rarely this straightforward.
Bending Stress in Beams
A more complex, yet incredibly important, scenario involves bending stress in beams. Beams are structural elements designed to withstand bending loads. The bending stress (σ) at a distance (y) from the neutral axis of the beam is given by: σ = My/I, where M is the bending moment, and I is the area moment of inertia. Themaximumbending stress occurs at the point furthest from the neutral axis, which is often at the top or bottom surface of the beam.
The Complete Bending Stress Formula
Therefore, themaximumbending stress (σmax) is: σmax = Mc/I, where 'c' is the distance from the neutral axis to the outermost fiber of the beam. This formula is crucial for designing beams that can safely carry bending loads, preventing structural failure. Understanding I, the area moment of inertia, is critical. It represents the beam's resistance to bending.
Example Calculation
Imagine a rectangular beam with a bending moment (M) of 500 Nm, a distance from the neutral axis to the outermost fiber (c) of 0.05 m, and an area moment of inertia (I) of
0.0001 m4. Using the formula σmax = Mc/I, the maximum bending stress would be: σmax = (500 Nm
0.05 m) /
0.0001 m4 = 250,000 N/m2 or 250 k Pa. This means the material at the outermost fiber is experiencing a stress of 250 k Pa.
Stress Concentrations: The Weak Links
Stress concentrations occur when there are geometric discontinuities in a component, such as holes, sharp corners, or changes in cross-section. At these points, the stress is significantly higher than the average stress in the surrounding area. Ignoring stress concentrations can lead to premature failure, even if the overall stress levels seem acceptable. These are common in components with threaded connections, for example.
The Stress Concentration Factor (Kt)
The stress concentration factor (Kt) is a multiplier that indicates how much higher the stress is at the point of concentration compared to the nominal stress. The maximum stress (σmax) at the stress concentration is: σmax = Kt σnominal, where σnominal is the stress calculated without considering the stress concentration. Values for Kt are typically obtained from charts or handbooks based on the geometry of the discontinuity.
Practical Implications
In practice, engineers need to carefully consider stress concentrations during the design phase. This often involves using fillets (rounded corners) instead of sharp corners, or using larger radii for holes. Finite element analysis (FEA) is also commonly used to identify and quantify stress concentrations in complex geometries. Addressing stress concentrations proactively is a key aspect of structural integrity.
Beyond the Basics: Advanced Considerations
While the formulas presented so far provide a solid foundation, real-world engineering problems often involve more complex loading scenarios and material behavior. Factors like fatigue, creep, and plasticity can significantly influence the maximum stress a component can withstand over its lifespan. Therefore, a solid understanding of material science and advanced analysis techniques are indispensable for any engineer involved in structural design or failure analysis.
Fatigue
Fatigue occurs when a material is subjected to repeated loading cycles. Even if the stress levels are below the material's yield strength, fatigue can lead to crack initiation and propagation, eventually resulting in failure. The maximum stress formula alone is insufficient to assess fatigue life; specialized fatigue analysis techniques are required.
Creep
Creep is the time-dependent deformation of a material under constant stress, especially at elevated temperatures. Components operating in high-temperature environments, such as gas turbine blades, are particularly susceptible to creep. Creep analysis requires considering both stress and temperature effects over extended periods.
Plasticity
The formulas we've discussed primarily apply to elastic behavior, where the material returns to its original shape after the load is removed. However, if the stress exceeds the material's yield strength, plastic deformation occurs. Understanding the plastic behavior of materials is crucial for designing components that can withstand overload conditions without catastrophic failure. This is where concepts like the ultimate tensile strength become vital.
Applications of Maximum Stress Formula in Engineering
The maximum stress formula is a fundamental tool applied across numerous engineering disciplines. Its application ensures the safety, reliability, and efficiency of structures and machines, highlighting its importance in the field.
Aerospace Engineering
In aerospace, this formula is used to design aircraft wings, fuselage, and engine components. Engineers calculate the maximum stress to ensure that these components can withstand aerodynamic forces, pressure changes, and temperature variations during flight. This calculation helps in selecting materials that are lightweight yet strong enough to endure extreme conditions.
Civil Engineering
Civil engineers use the formula to design bridges, buildings, and dams. They assess the maximum stress to ensure that these structures can withstand the weight of traffic, environmental loads (wind, snow, earthquakes), and water pressure. This helps to guarantee the longevity and safety of infrastructure projects.
Mechanical Engineering
Mechanical engineers apply the maximum stress formula in designing machine parts, engines, and pressure vessels. They calculate the maximum stress to ensure that these components can withstand the mechanical loads, thermal stresses, and internal pressures they encounter. This is crucial for the performance and durability of machinery.
Automotive Engineering
In the automotive industry, the maximum stress formula is utilized to design car chassis, suspension systems, and engine parts. Engineers ensure that these components can endure the stresses from driving, braking, and collisions. This helps to enhance vehicle safety and performance.
Pros and Cons of Using Maximum Stress Formula
Like any engineering tool, the maximum stress formula has both advantages and limitations. Understanding these pros and cons can guide engineers in its proper application.
Pros
- Provides a fundamental understanding of material behavior under stress.
- Enables preliminary design and material selection decisions.
- Offers a simplified approach to estimate stress levels in simple geometries.
- Is cost-effective for initial assessments before detailed analysis.
Cons
- May not accurately represent complex loading conditions or geometries.
- Does not account for material imperfections, residual stresses, or environmental factors.
- Requires assumptions that may not always hold true in real-world applications.
- Can be less accurate for dynamic loads, fatigue, or creep conditions.
Using FEA to Supplement the Formula
Finite Element Analysis (FEA) offers a robust supplement to the maximum stress formula, particularly when dealing with complex geometries and loading conditions where the formula's simplifications fall short. FEA enables engineers to simulate real-world scenarios by dividing a structure into many smaller elements. By using FEA, engineers can accurately map stress distributions, predict failure points, and refine designs, which can lead to more efficient and reliable engineering solutions.
Frequently Asked Questions (FAQs)
What is the difference between stress and strain?
Stress is the force per unit area within a material, while strain is the deformation of the material caused by that stress. Stress is the cause, and strain is the effect.
How do I determine the area moment of inertia (I) for different shapes?
The area moment of inertia depends on the shape's geometry. For a rectangle, I = (bh3)/12, where b is the base and h is the height. For a circle, I = (πd4)/64, where d is the diameter. Standard formulas exist for common shapes, and handbooks provide values for more complex sections.
What is the factor of safety, and how does it relate to the maximum stress formula?
The factor of safety (FOS) is a multiplier applied to the allowable stress to ensure a component's safe operation. Allowable Stress = Material Strength / FOS. A higher FOS indicates a more conservative design.
When should I use FEA instead of relying solely on the maximum stress formula?
Use FEA when dealing with complex geometries, non-uniform loading, stress concentrations, or when you need a more accurate stress distribution. It's also essential for fatigue, creep, or dynamic analysis.
How does temperature affect the maximum stress a material can withstand?
Temperature can significantly affect a material's strength and stiffness. Generally, higher temperatures reduce the yield strength and ultimate tensile strength, making the material more susceptible to failure at lower stress levels. Creep becomes a significant factor at elevated temperatures.
What are some common mistakes to avoid when using the maximum stress formula?
Common mistakes include neglecting stress concentrations, using incorrect formulas for the geometry, failing to consider the correct loading conditions, and not accounting for material properties at the operating temperature. Double-checking your assumptions and calculations is crucial.
Conclusion
The maximum stress formula is an indispensable tool in the world of mechanics, vital for ensuring structural integrity and safety. While it provides a powerful foundation for understanding stress in materials, it's crucial to remember its limitations and to supplement it with advanced techniques like FEA when necessary. Master this formula, and you'll be well on your way to designing safer, more reliable structures and machines. Keep learning, keep exploring, and keep building!
Posting Komentar untuk "Derivation of Maximum Stress Formula in Mechanics"