Applications of Hoop Stress Formula in Pressure Vessels
Ever wondered how a scuba tank withstands the immense pressure deep underwater, or how pipelines safely transport natural gas across vast distances? The secret lies in understanding and applying the principles of hoop stress. As mechanical engineers and professionals involved in structural design, grasping the hoop stress formula is crucial for ensuring the safety and reliability of pressure vessels. This knowledge allows us to predict how these containers will respond under pressure and prevent potential failures, safeguarding both infrastructure and lives.
Understanding Hoop Stress
Hoop stress, also known as circumferential stress, is the force exerted tangentially within the walls of a pressure vessel. Imagine slicing a pipe lengthwise; hoop stress is what prevents the two halves from separating under internal pressure. It's a critical factor in determining the required material strength and thickness of a vessel.
Essentially, hoop stress arises because the internal pressure pushes outward against the vessel walls. This outward force is resisted by the tensile strength of the material, resulting in stress that acts circumferentially around the vessel.
Hoop Stress Formula Derivation
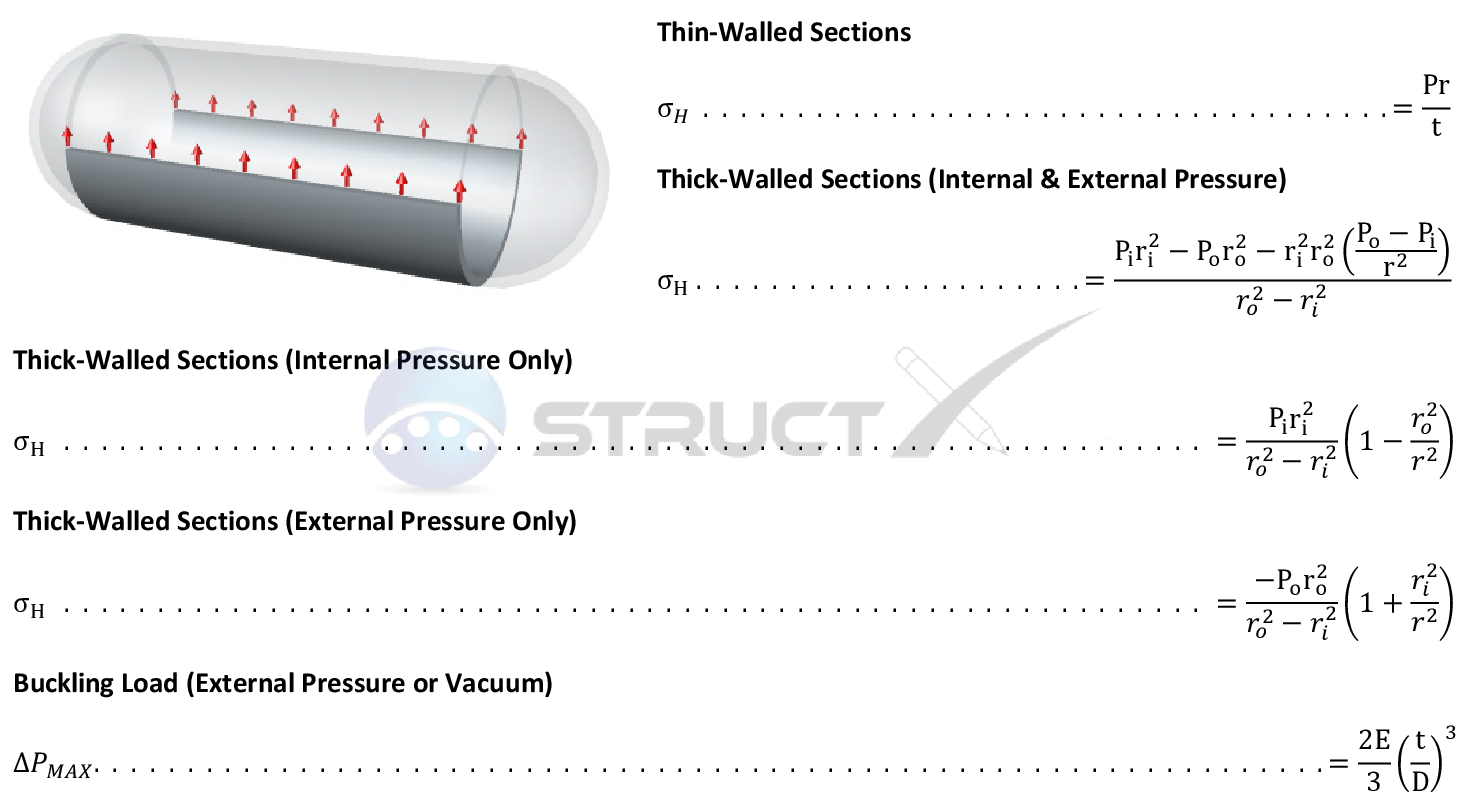
The formula for hoop stress (σh) in a thin-walled pressure vessel can be derived through a force balance analysis. Consider a cylindrical vessel with internal pressure (p), radius (r), and wall thickness (t). We can isolate a section of the cylinder and analyze the forces acting on it.
The force due to the internal pressure acting on the projected area is given by: Fp = p (2r L), where L is the length of the cylinder section.
This force is resisted by the hoop stress acting on the cross-sectional area of the vessel wall: Fσ = 2 (σh t L).
Equating these two forces (Fp = Fσ) and solving for hoop stress, we get:
σh = (p r) / t
This formula is fundamental for calculating the hoop stress in thin-walled cylindrical pressure vessels.
Practical Applications of the Hoop Stress Formula
The hoop stress formula is not just a theoretical concept; it has numerous real-world applications in the design, analysis, and maintenance of pressure vessels across various industries. From pipelines to storage tanks, understanding hoop stress is essential for ensuring structural integrity.
Here, we discuss a few examples:
Pipeline Design and Analysis
Pipelines transporting oil, natural gas, and other fluids are subjected to significant internal pressure. The hoop stress formula is used to determine the required wall thickness of the pipe based on the operating pressure and the pipe's diameter. Accurate hoop stress calculations are vital to prevent pipeline ruptures and leaks, ensuring safe and efficient transport of these valuable resources.
Pressure Vessel Design for Chemical Plants
Chemical plants often employ pressure vessels to store and process various chemicals under high pressure and temperature. The hoop stress formula helps engineers determine the appropriate material and wall thickness for these vessels, taking into account factors such as corrosion resistance and safety margins. Proper design ensures the containment of hazardous materials and prevents catastrophic failures.
Compressed Gas Cylinders (Scuba Tanks, Oxygen Tanks)
Scuba tanks and oxygen tanks are designed to withstand very high internal pressures. The hoop stress formula is crucial in determining the minimum wall thickness necessary to contain the compressed gas safely. These calculations ensure that the tanks can withstand the stresses imposed during filling, storage, and use, preventing explosions and injuries.
Boiler Design
Boilers, used for steam generation in power plants and heating systems, are another critical application of hoop stress calculations. The high pressure inside the boiler demands careful consideration of material strength and wall thickness to prevent catastrophic failures. The hoop stress formula assists in designing robust and reliable boilers capable of withstanding the extreme operating conditions.
Hoop Stress vs. Longitudinal Stress
While hoop stress acts circumferentially, longitudinal stress acts along the length of the pressure vessel. Both types of stress are important, but they differ in magnitude. For a cylindrical vessel, the longitudinal stress is typically half the hoop stress: σl = (p r) / (2t). This difference arises because the longitudinal stress acts on the entire cross-sectional area of the vessel, while the hoop stress acts on a smaller area.
Understanding the relationship between hoop stress and longitudinal stress is important for comprehensive stress analysis and failure analysis. Both stresses must be considered during the design phase to ensure the overall structural integrity of the pressure vessel.
Factors Affecting Hoop Stress
Several factors can influence the magnitude of hoop stress in a pressure vessel. These factors must be carefully considered during design and operation to ensure safe performance.
- Internal Pressure (p): A higher internal pressure directly increases the hoop stress.
- Radius of the Vessel (r): A larger radius also increases the hoop stress.
- Wall Thickness (t): A thicker wall reduces the hoop stress.
- Material Strength: The material's tensile strength must be sufficient to withstand the hoop stress.
- Temperature: Elevated temperatures can reduce the material's strength, increasing the risk of failure.
- Corrosion: Corrosion can thin the vessel wall, increasing the hoop stress and weakening the structure.
Accounting for these factors is crucial for accurate hoop stress calculations and safe pressure vessel design.
Limitations of the Hoop Stress Formula
While the hoop stress formula (σh = (p r) / t) is a valuable tool, it's essential to recognize its limitations. This formula is primarily applicable tothin-walledpressure vessels, where the wall thickness (t) is significantly smaller than the radius (r) (typically t/r < 0.1).
For thick-walled pressure vessels, the stress distribution across the wall thickness is no longer uniform, and more complex stress analysis methods, such as Lame's equations, are required. Furthermore, the formula assumes a uniform internal pressure and a perfectly cylindrical shape. Any irregularities, such as nozzles or welds, can create stress concentrations that are not accounted for by the simple hoop stress formula.
FAQ Section
What is the difference between hoop stress and axial stress?
Hoop stress (or circumferential stress) acts tangentially around the circumference of the pressure vessel, resisting the bursting force due to internal pressure. Axial stress (or longitudinal stress) acts along the length of the vessel.
When should I use Lame's equation instead of the hoop stress formula?
Lame's equation should be used for thick-walled pressure vessels (typically where the ratio of wall thickness to radius is greater than 0.1). The hoop stress formula is accurate only for thin-walled vessels.
How does temperature affect hoop stress calculations?
Temperature can affect the material properties of the pressure vessel, such as its tensile strength. At higher temperatures, the tensile strength may decrease, which can increase the risk of failure even if the hoop stress itself remains the same. Temperature effects must be considered in material selection and design.
Can corrosion affect the hoop stress in a pressure vessel?
Yes, corrosion can reduce the wall thickness of the pressure vessel. This reduction in thickness directly increases the hoop stress according to the formula σh = (p r) / t. Regular inspections and maintenance are critical to detect and address corrosion.
What are some common causes of pressure vessel failure related to hoop stress?
Common causes include exceeding the design pressure, corrosion-induced thinning of the vessel wall, manufacturing defects (such as welds), and operating the vessel at temperatures above its design limits.
How is the factor of safety applied when using the hoop stress formula?
A factor of safety is applied to the calculated hoop stress to ensure a margin of safety. This involves selecting a material with a tensile strength significantly higher than the calculated hoop stress, divided by the desired factor of safety. The appropriate factor of safety depends on the application, industry standards, and regulatory requirements.
Conclusion
The hoop stress formula is a cornerstone of pressure vessel design, analysis, and maintenance. By understanding the principles behind this formula, engineers can ensure the safe and reliable operation of a wide range of critical infrastructure components. While it's essential to be aware of its limitations, the hoop stress formula provides a valuable tool for predicting and preventing failures, ultimately protecting both people and property. Continue to deepen your understanding of related concepts like tensile and compressive stress, failure analysis and material strength; your expertise can make a real difference in the field of mechanical engineering.
Posting Komentar untuk "Applications of Hoop Stress Formula in Pressure Vessels"