Compressive Stress Formula Explained with Examples
Ever wondered why bridges can withstand tons of weight, or how skyscrapers don't crumble under their own mass? Compressive stress, the force squeezing a material, plays a huge role. For engineers, understanding this principle is fundamental for designing safe and efficient structures. For students diving into mechanical engineering, it's a key concept to master for analyzing material strength. And for anyone in the field, a solid grasp of compressive stress is essential for preventing catastrophic failures. Let's break down the formula and see how it works in the real world.
Understanding Compressive Stress
Compressive stress arises when forces push or squeeze an object, causing it to deform or compress. Think of squeezing a sponge or the legs of a table supporting a heavy object. This is the opposite of tensile stress, which occurs when forces pull or stretch an object. Understanding the difference between tensile and compressive stress is crucial for material strength analysis.
The compressive stress formula helps us quantify the amount of force acting on a material's cross-sectional area, providing vital insights into its structural integrity. By calculating compressive stress, engineers can predict how a material will respond under load and design accordingly, preventing potential failures.
The Compressive Stress Formula
The formula for compressive stress is surprisingly straightforward:
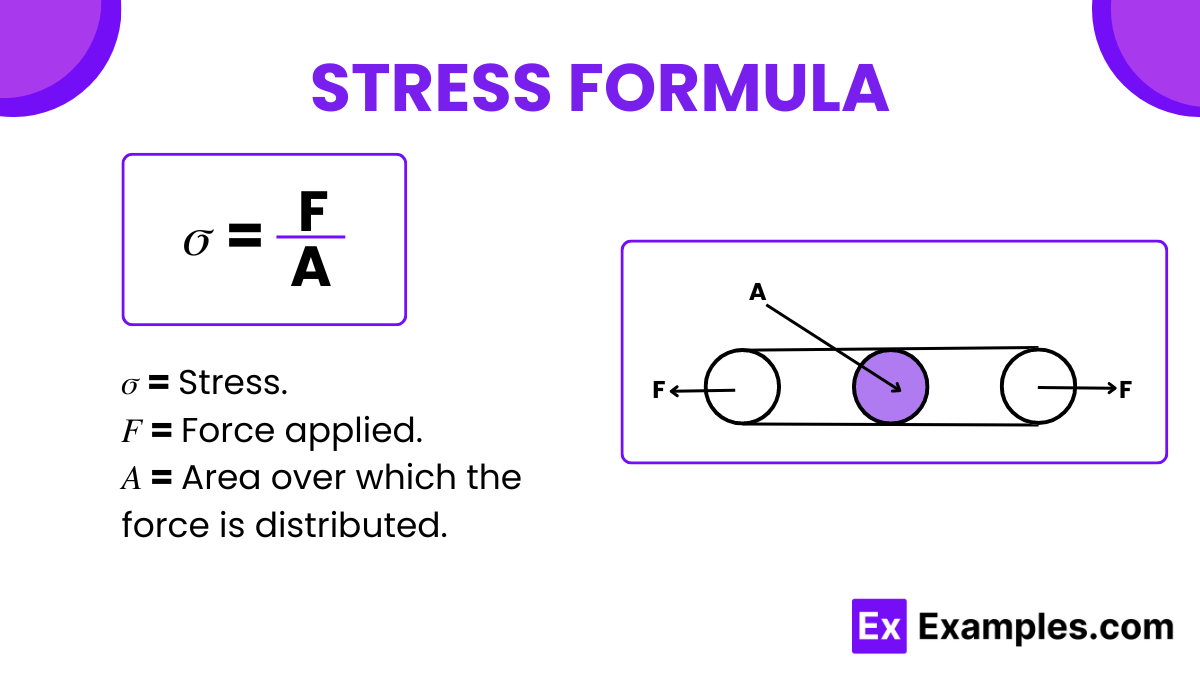
σ = F/A
Where:
- σ (sigma) represents the compressive stress, usually measured in Pascals (Pa) or pounds per square inch (psi).
- F is the compressive force applied, measured in Newtons (N) or pounds (lb).
- A is the cross-sectional area of the material that is perpendicular to the force, measured in square meters (m²) or square inches (in²).
Essentially, you're dividing the force pressing down on the object by the area over which that force is distributed. This gives you the compressive stress experienced by the material.
Deriving the Formula
The formula stems from the fundamental definition of stress as force per unit area. Imagine a column supporting a weight. The weight (force) is distributed across the column's top surface (area). The stress is simply the measure of how concentrated that force is across that area. A larger area means the force is distributed more evenly, resulting in lower stress.
Compressive Stress Examples and Calculations
Let's put the formula into practice with a few examples. These examples demonstrate how compressive stress calculations apply to real-world scenarios.
Example 1: Concrete Column
A concrete column with a cross-sectional area of 0.25 m² supports a compressive load of 500,000 N. Calculate the compressive stress on the column.
σ = F/A = 500,000 N / 0.25 m² = 2,000,000 Pa or 2 MPa.
This means the concrete is experiencing a compressive stress of 2 MPa.
Example 2: Wooden Block
A wooden block with dimensions 10 cm x 10 cm is subjected to a compressive force of 10,000 N. Find the compressive stress.
First, calculate the area: A = 0.1 m x
0.1 m =
0.01 m².
Then, calculate the stress: σ = F/A = 10,000 N / 0.01 m² = 1,000,000 Pa or 1 MPa.
The wooden block is under a compressive stress of 1 MPa.
Example 3: Steel Rod
A steel rod with a diameter of 2 cm is compressed with a force of 20,000 N. Calculate the compressive stress.
First, find the radius: r = diameter / 2 = 1 cm = 0.01 m.
Then, calculate the area: A = πr² = π (0.01 m)² ≈
0.000314 m².
Finally, calculate the stress: σ = F/A = 20,000 N / 0.000314 m² ≈ 63,694,267.52 Pa or approximately
63.7 MPa.
The steel rod is experiencing a significant compressive stress of about 63.7 MPa.
Practical Applications of Compressive Stress
Compressive stress considerations are vital in numerous fields. The applications are extensive, from civil engineering to aerospace.
- Civil Engineering: Designing bridges, buildings, and tunnels to withstand compressive forces from their own weight and external loads.
- Mechanical Engineering: Analyzing the stress on machine components like pistons, gears, and bearings.
- Aerospace Engineering: Ensuring aircraft structures can handle compressive loads during flight.
- Material Science: Studying the behavior of materials under compression to determine their strength and durability.
Pros and Cons of High Compressive Strength Materials
Materials with high compressive strength, like concrete and steel, are widely used in construction and engineering. However, it's important to consider both their advantages and disadvantages.
Pros:
- High Load-Bearing Capacity: Can support substantial weight without failure.
- Durability: Resistant to deformation and cracking under compressive loads.
- Versatility: Suitable for a wide range of applications in construction, manufacturing, and infrastructure.
Cons:
- Brittle Failure: Some high-strength materials can fail suddenly without warning signs.
- Tensile Weakness: Often exhibit lower tensile strength compared to compressive strength, requiring reinforcement in applications with tensile forces.
- Cost: High-performance materials can be expensive, increasing overall project costs.
Compressive Stress vs. Tensile Stress
Compressive and tensile stresses are fundamental concepts in material science and structural design. It is useful to understand the differences.
Compressive Stress: Occurs when a material is squeezed or compressed, reducing its volume. The forces act inward, pushing the material together.
Tensile Stress: Occurs when a material is stretched or pulled, increasing its length. The forces act outward, pulling the material apart.
Materials respond differently to these two types of stress. Concrete, for example, is strong in compression but weak in tension. Steel, on the other hand, has good strength in both tension and compression. Understanding these differences is crucial for selecting the right material for a specific application and ensuring structural integrity.
Failure Analysis and Compressive Stress
Compressive stress plays a significant role in failure analysis. When a structure collapses or a component breaks, it's often due to exceeding the material's compressive strength. By analyzing the stress distribution and comparing it to the material's properties, engineers can identify the root cause of the failure and implement preventative measures.
This analysis often involves calculating the compressive stress at critical points in the structure and comparing it to the material's compressive strength. If the stress exceeds the strength, it indicates a potential failure point. Understanding compressive stress is therefore essential for conducting thorough and accurate failure analysis.
FAQ on Compressive Stress
What are the units for compressive stress?
The most common units are Pascals (Pa) in the metric system and pounds per square inch (psi) in the imperial system.
How does temperature affect compressive strength?
Generally, compressive strength decreases with increasing temperature. Elevated temperatures can weaken the material's structure, making it more susceptible to deformation and failure under compressive loads.
What is compressive strain?
Compressive strain is the measure of deformation that a material undergoes when subjected to compressive stress. It's calculated as the change in length divided by the original length.
What materials have high compressive strength?
Concrete, steel, granite, and diamond are examples of materials with high compressive strength.
Is compressive stress always a bad thing?
Not necessarily. Compressive stress is often utilized in structural design to enhance stability and load-bearing capacity. However, excessive compressive stress can lead to failure.
How can I improve a material's compressive strength?
Methods include using stronger materials, increasing the cross-sectional area, and applying pre-stressing techniques.
Conclusion
Understanding the compressive stress formula is critical for engineers, students, and anyone involved in structural design or material analysis. By grasping the principles behind compressive stress and how to calculate it, you can ensure structures are safe, durable, and capable of withstanding the forces they're designed to bear. Keep practicing with examples and exploring real-world applications to solidify your knowledge and confidently tackle complex engineering challenges!
Posting Komentar untuk "Compressive Stress Formula Explained with Examples"