Hoop Stress Formula Explained with Step-by-Step Examples

Ever wondered why a pipe bursts along its length rather than circumferentially? The answer lies in hoop stress, a critical concept in mechanical engineering, especially when dealing with pressure vessels, pipes, and tanks. Understanding and accurately calculating hoop stress is paramount for ensuring the structural integrity and safety of these systems. Incorrect calculations can lead to catastrophic failures, making this a vital skill for engineers and anyone involved in structural design.

What is Hoop Stress? A Deep Dive

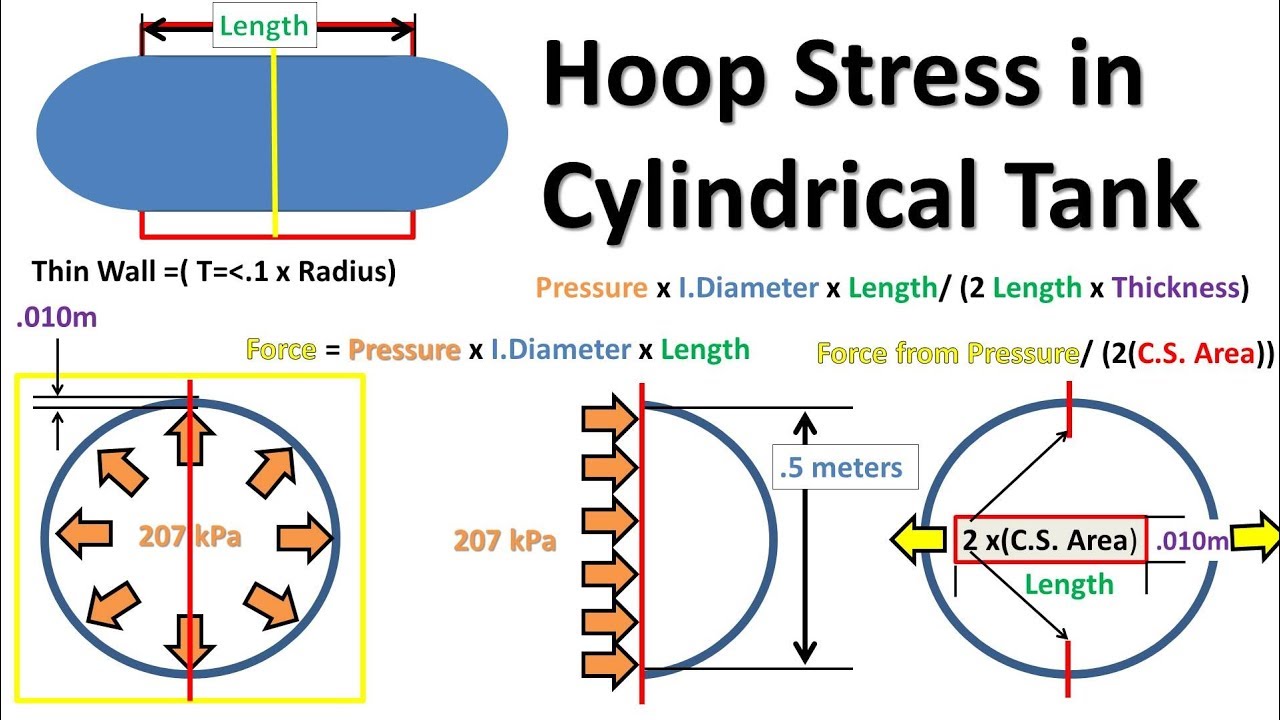
Hoop stress, also known as circumferential stress, is the force exerted tangentially on the circumference of a cylindrical object caused by internal pressure. Imagine a water pipe: the water pressure inside pushes outwards, creating tension within the pipe wall. This tension acts around the circumference of the pipe, trying to expand it. This is hoop stress.

Hoop stress is directly proportional to the internal pressure and the radius of the cylinder, and inversely proportional to the wall thickness. In simpler terms, a higher pressure, a larger radius, or a thinner wall will result in a greater hoop stress. This is a fundamental principle for understanding the behavior of pressure vessels under load.

It is crucial to distinguish hoop stress from other types of stress, such as longitudinal stress (acting along the length of the cylinder) and radial stress (acting through the thickness of the cylinder). While all three stresses are present in a pressurized cylinder, hoop stress is often the most significant and dictates the design considerations to prevent failure.

The Hoop Stress Formula: Unveiled

The formula for calculating hoop stress is relatively straightforward, making it an essential tool for engineers. Here's the standard equation:

σ_h = (P r) / t

Where:

1. σ_h represents the hoop stress (typically measured in Pascals (Pa) or pounds per square inch (psi)).
1. P represents the internal pressure (typically measured in Pascals (Pa) or pounds per square inch (psi)).
1. r represents the internal radius of the cylinder (typically measured in meters (m) or inches (in)).
1. t represents the wall thickness of the cylinder (typically measured in meters (m) or inches (in)).

This formula assumes a thin-walled cylinder, meaning the wall thickness is significantly smaller than the radius (typically, t < r/10). For thick-walled cylinders, more complex formulas are required to account for the variation of stress across the wall thickness. We'll focus on the thin-walled cylinder case for simplicity and its common application.

Step-by-Step Examples: Calculating Hoop Stress

Let's solidify our understanding with some practical examples. We'll work through two scenarios, providing a step-by-step breakdown of the calculations.

Example 1: Calculating Hoop Stress in a Water Pipe

A steel water pipe has an internal diameter of 0.5 meters and a wall thickness of 10 mm. The water pressure inside the pipe is

1.5 MPa. Calculate the hoop stress in the pipe wall.

Step 1: Convert units to be consistent.

1. Radius (r) = Diameter / 2 = 0.5 m / 2 =

0.25 m

1. Thickness (t) = 10 mm = 0.01 m

1. Pressure (P) = 1.5 MPa =

1.5 x 10⁶ Pa

Step 2: Apply the hoop stress formula.

σ_h = (P r) / t = (1.5 x 10⁶ Pa

0.25 m) /

0.01 m

Step 3: Calculate the hoop stress.

σ_h = 37.5 x 10⁶ Pa =

37.5 MPa

Therefore, the hoop stress in the water pipe wall is 37.5 MPa.

Example 2: Determining Wall Thickness for a Pressure Vessel

A cylindrical pressure vessel with an internal radius of 1 meter needs to withstand an internal pressure of 5 MPa. The allowable tensile stress for the material is 100 MPa. Calculate the required wall thickness of the pressure vessel.

Step 1: Rearrange the hoop stress formula to solve for thickness (t).

t = (P r) / σ_h

Step 2: Plug in the given values.

t = (5 x 10⁶ Pa 1 m) / (100 x 10⁶ Pa)

Step 3: Calculate the required wall thickness.

t = 0.05 m = 50 mm

Therefore, the required wall thickness for the pressure vessel is 50 mm to safely withstand the internal pressure, given the material's allowable stress.

Factors Affecting Hoop Stress

Several factors can influence the actual hoop stress experienced by a cylindrical object. It's important to consider these factors during the design and analysis process.

1. Material Properties: The material's tensile strength plays a crucial role. The hoop stress must remain below the material's yield strength to prevent permanent deformation and below the ultimate tensile strength to avoid fracture.
1. Temperature: Temperature variations can affect the material's properties and induce thermal stresses, which can add to the hoop stress.
1. Corrosion: Corrosion can reduce the wall thickness over time, increasing the hoop stress and potentially leading to failure.
1. Welding and Manufacturing Processes: Imperfections or residual stresses introduced during welding or manufacturing can significantly affect the hoop stress distribution and overall structural integrity.
1. External Loads: External forces or moments acting on the cylinder can create additional stresses that must be considered alongside the hoop stress.

Practical Applications of Hoop Stress Calculation

The hoop stress formula finds widespread application in various engineering fields. Understanding hoop stress is critical in the design and maintenance of various systems.

1. Pipeline Design: Calculating hoop stress is essential for designing safe and reliable pipelines for transporting oil, gas, and water.
1. Pressure Vessel Design: Pressure vessels, such as boilers and storage tanks, require accurate hoop stress calculations to ensure they can safely contain high-pressure fluids or gases.
1. Hydraulic Cylinders: The design of hydraulic cylinders relies on hoop stress calculations to determine the required wall thickness to withstand the hydraulic pressure.
1. Tire Design: Although not a perfect cylinder, the principles of hoop stress are used in analyzing the stresses within a tire under inflation.
1. Aerospace Engineering: Hoop stress considerations are crucial in the design of aircraft fuselages and rocket motor casings.

Limitations of the Thin-Walled Cylinder Assumption

As mentioned earlier, the simple hoop stress formula is based on the assumption of a thin-walled cylinder. This assumption is valid when the wall thickness is relatively small compared to the radius (typically, t < r/10). When the wall thickness becomes significant (thick-walled cylinders), the stress distribution across the wall is no longer uniform, and the simple formula becomes inaccurate.

For thick-walled cylinders, more complex formulas, such as the Lamé equations, are required to accurately calculate the stress distribution. These equations account for the variation of radial and hoop stress across the cylinder wall.

Ignoring the limitations of the thin-walled cylinder assumption can lead to significant errors in stress calculations and potentially unsafe designs. Therefore, it's crucial to assess the validity of the assumption before applying the simple hoop stress formula.

Tensile and Compressive Stress: The Role of Hoop Stress

Hoop stress is a tensile stress, meaning it acts to pull the material apart. In the case of a pressurized cylinder, the internal pressure is trying to expand the cylinder, creating tension in the circumferential direction. This tensile stress is what we refer to as hoop stress.

While hoop stress is tensile, compressive stress can also play a role in structural design. For example, external pressure on a cylinder would induce compressive hoop stress. It is crucial to understand if the material is better suited to tensile or compressive forces, and designing accordingly is paramount to structural integrity.

Failure Analysis and Hoop Stress

Hoop stress is a critical consideration in failure analysis. When a cylindrical object fails under internal pressure, it typically fails along its length due to the high tensile hoop stress. By analyzing the failure mode and calculating the hoop stress at the point of failure, engineers can determine the root cause of the failure and implement measures to prevent similar failures in the future. This is a standard procedure in mechanical engineering.

Advantages and Disadvantages of Using the Hoop Stress Formula

Like any engineering tool, the hoop stress formula has its advantages and disadvantages. It is important to be mindful of these when applying this formula.

Advantages

1. Simplicity: The formula is straightforward and easy to apply, making it a valuable tool for quick estimations and preliminary design calculations.
1. Wide Applicability: It is applicable to a wide range of cylindrical structures, including pipes, pressure vessels, and hydraulic cylinders.
1. Fundamental Understanding: It provides a fundamental understanding of the relationship between pressure, radius, thickness, and stress in cylindrical structures.

Disadvantages

1. Thin-Walled Assumption: It is based on the assumption of a thin-walled cylinder, which limits its accuracy for thick-walled cylinders.
1. Ignores Other Stresses: It only considers hoop stress and ignores other stresses, such as longitudinal and radial stresses, which can also contribute to failure.
1. Idealized Conditions: It assumes idealized conditions and does not account for factors such as material imperfections, corrosion, and welding residual stresses.

Frequently Asked Questions (FAQs)

What is the difference between hoop stress and longitudinal stress?

Hoop stress acts circumferentially around a cylinder due to internal pressure, while longitudinal stress acts along the length of the cylinder. Longitudinal stress is typically half the magnitude of hoop stress in a thin-walled cylinder.

How does temperature affect hoop stress?

Temperature changes can cause the material to expand or contract, inducing thermal stresses that add to the hoop stress caused by internal pressure. High temperatures can also weaken the material, reducing its allowable stress.

What happens if the hoop stress exceeds the material's tensile strength?

If the hoop stress exceeds the material's tensile strength, the cylinder will likely fracture along its length due to excessive tensile stress. This is a critical design consideration for pressure vessels and pipelines.

Can the hoop stress formula be used for non-cylindrical shapes?

No, the hoop stress formula is specifically derived for cylindrical shapes. For non-cylindrical shapes, more complex stress analysis techniques, such as finite element analysis (FEA), are required.

What safety factor should I use when calculating hoop stress for design purposes?

The safety factor depends on the application and the potential consequences of failure. Typically, a safety factor of 2 to 4 is used for pressure vessels and pipelines, but this can vary based on regulations and industry standards. Consult with an experienced engineer and relevant codes.

Is hoop stress always tensile?

No, hoop stress can be tensile (pulling) or compressive (pushing). Internal pressure in a cylinder creates tensile hoop stress, while external pressure creates compressive hoop stress.

Conclusion: Mastering Hoop Stress for Safe Engineering Design

Understanding and accurately calculating hoop stress is essential for ensuring the safety and reliability of pressure vessels, pipelines, and other cylindrical structures. While the simple hoop stress formula provides a valuable tool for preliminary design and analysis, it's crucial to be aware of its limitations and consider other factors that can influence the actual stress distribution. Always remember to account for material properties, temperature effects, corrosion, and welding imperfections. By mastering the principles of hoop stress, engineers can design safer and more robust systems, preventing catastrophic failures and protecting human lives.

```