Thick Cylinder Stress Formula with Examples
Ever wondered how pipelines withstand immense pressure, or how hydraulic cylinders manage to lift tons of weight without bursting? The secret lies in understanding the stresses within thick cylinders. Unlike thin-walled pressure vessels, thick cylinders experience significant stress variations across their walls, requiring a more complex analysis. This knowledge is crucial for engineers designing everything from submarines to high-pressure reactors, ensuring safety and reliability. Let's dive into the fascinating world of thick cylinder stress!
Understanding Thick vs. Thin Cylinders
Before we get into the formulas, let’s clarify the difference between thick and thin cylinders. It’s all about the ratio of the cylinder's wall thickness (t) to its inner radius (ri). A cylinder is generally considered "thin" if t/ri is less than 0.1. In thin cylinders, we can assume that the stress is uniformly distributed across the wall thickness. However, when t/ri exceeds
0.1, the stress distribution becomes non-uniform, and we must treat it as a thick cylinder.
Failing to account for the varying stresses in a thick cylinder can lead to inaccurate predictions of its strength and potentially catastrophic failure. This is why understanding and applying the correct stress formulas is paramount in mechanical engineering.
Lame's Equations: The Foundation
The cornerstone of thick cylinder stress analysis is Lame's equations. These equations allow us to calculate the radial and hoop (circumferential) stresses at any point within the cylinder wall.
Radial Stress
The radial stress (σr) is the stress acting perpendicular to the cylindrical surface at a given radius (r). Lame's equation for radial stress is:
σr = B/r² - A
Where:
- σr is the radial stress
- r is the radius at the point of interest
- A and B are constants of integration determined by boundary conditions
Hoop Stress
The hoop stress (σθ), also known as circumferential stress, acts tangentially to the cylindrical surface. Lame's equation for hoop stress is:
σθ = B/r² + A
Where:
- σθ is the hoop stress
- r is the radius at the point of interest
- A and B are constants of integration determined by boundary conditions
Determining Constants A and B
To use Lame's equations, we need to find the constants A and B. This is done by applying boundary conditions, which typically involve knowing the internal pressure (pi) at the inner radius (ri) and the external pressure (po) at the outer radius (ro).
The boundary conditions are:
- At r = ri, σr = -pi (negative because pressure is compressive)
- At r = ro, σr = -po (negative because pressure is compressive)
Substituting these boundary conditions into the radial stress equation, we get two equations that we can solve simultaneously for A and B:
-pi = B/ri² - A
-po = B/ro² - A
Solving these equations for A and B yields:
A = (piri² - poro²) / (ro² - ri²)
B = ri²ro² (pi - po) / (ro² - ri²)
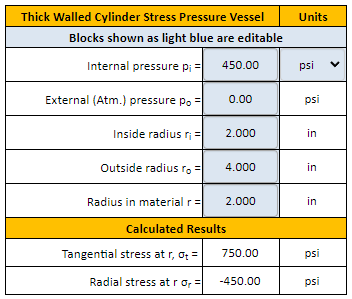
Example Calculation
Let's consider a steel cylinder with an inner radius (ri) of 50 mm and an outer radius (ro) of 100 mm. The internal pressure (pi) is 50 MPa, and the external pressure (po) is 0 MPa.
First, calculate A and B:
A = (50 50² - 0 100²) / (100² - 50²) = (50 2500) / (10000 - 2500) = 125000 / 7500 = 16.67 MPa
B = 50² 100² (50 - 0) / (100² - 50²) = 2500 10000 50 / 7500 = 1250000000 / 7500 = 166666.67 MPa.mm²
Now, let's find the radial and hoop stresses at the inner radius (r = 50 mm):
σr = 166666.67 / 50² -
16.67 =
166666.67 / 2500 -
16.67 =
66.67 -
16.67 = 50 MPa (compressive, as expected, and equals -pi)
σθ = 166666.67 / 50² +
16.67 =
66.67 +
16.67 =
83.34 MPa (tensile)
Now, let's find the radial and hoop stresses at the outer radius (r = 100 mm):
σr = 166666.67 / 100² -
16.67 =
166666.67 / 10000 -
16.67 =
16.67 -
16.67 = 0 MPa (compressive, as expected, and equals -po)
σθ = 166666.67 / 100² +
16.67 =
16.67 +
16.67 =
33.34 MPa (tensile)
Notice how the hoop stress is highest at the inner radius and decreases towards the outer radius. This is a characteristic of thick cylinders under internal pressure.
Practical Applications
Thick cylinder stress analysis is crucial in various engineering fields. Here are a few examples:
- Pressure Vessels: Designing safe and reliable pressure vessels for chemical plants, power plants, and oil refineries.
- Hydraulic Cylinders: Ensuring hydraulic cylinders can withstand the immense pressures required to operate heavy machinery.
- Gun Barrels: Analyzing stresses in gun barrels during firing to prevent failure.
- Submarines: Evaluating the structural integrity of submarine hulls under deep-sea pressure.
Pros and Cons of Thick Cylinder Design
Pros:
- High-Pressure Capacity: Thick cylinders can withstand significantly higher internal pressures compared to thin cylinders.
- Durability: The increased wall thickness provides enhanced resistance to deformation and failure.
Cons:
- Weight and Material Cost: Thick cylinders require more material, increasing their weight and cost.
- Complex Manufacturing: Manufacturing thick cylinders can be more challenging due to the larger dimensions and material requirements.
Beyond Lame's Equations
While Lame's equations provide a solid foundation, more advanced analysis techniques may be necessary for complex geometries or loading conditions. Finite element analysis (FEA) is a powerful tool for simulating stress distributions in complex thick cylinder designs, allowing for optimization and validation of structural integrity.
FAQs
What is the difference between hoop stress and longitudinal stress in a cylinder?
Hoop stress acts circumferentially, resisting the bursting force from internal pressure. Longitudinal stress acts along the length of the cylinder, resisting the force trying to pull the cylinder apart lengthwise. In thin cylinders, longitudinal stress is half the hoop stress. In thick cylinders, the relationship is more complex.
How does autofrettage improve the strength of a thick cylinder?
Autofrettage is a process where the cylinder is subjected to internal pressure exceeding its yield strength. This creates residual compressive stresses at the inner wall, which help to counteract the tensile stresses induced during normal operation, thereby increasing the cylinder's pressure capacity and fatigue life.
What materials are commonly used for thick cylinders?
High-strength steels are the most common materials for thick cylinders due to their ability to withstand high stresses. Other materials, such as titanium alloys and composite materials, may be used in specialized applications where weight is a critical factor.
How does temperature affect the stress distribution in a thick cylinder?
Temperature gradients across the cylinder wall can induce thermal stresses, which must be considered in addition to the pressure-induced stresses. These thermal stresses can significantly affect the overall stress distribution and the cylinder's structural integrity.
What is the significance of Tresca and Von Mises yield criteria in thick cylinder design?
Tresca and Von Mises yield criteria are used to predict when a material will start to yield under complex stress states. In thick cylinder design, these criteria are used to ensure that the calculated stresses remain below the material's yield strength, preventing permanent deformation and failure.
How can I validate my thick cylinder stress calculations?
You can validate your calculations through experimental testing, such as strain gauge measurements, or by using finite element analysis (FEA) software to simulate the stress distribution and compare the results with your analytical calculations.
Conclusion
Understanding thick cylinder stress is crucial for designing safe and efficient pressure-bearing components. By mastering Lame's equations and considering the various factors that influence stress distribution, engineers can ensure the structural integrity of critical systems across diverse industries. Keep practicing, exploring, and applying these principles, and you'll be well on your way to becoming a proficient structural design expert!
Posting Komentar untuk "Thick Cylinder Stress Formula with Examples"